

CONTINA AG, VADUZ
Principality of Liechtenstein (economic and customs union with Switzerland)
Every example in this collection relates to both CURTA models, with
the exception of those which are
marked "only CURTA Model II". The two machines differ only in
the number of figures which they can
handle. These are:
Setting Counter
Result
Register Register
Register
for the CURTA Model I
8
6
11
for the CURTA Model II
11
8
15
In every example the following abbreviations are used:
S.R. = Setting Register;
C.R. = Counter Register;
R.R. = Result Register.
The expression "Machine ready" signifies that:
(5 or 6 figures are required in the answer.)
Machine ready.
To begin with it is necessary to add together the three terms in the
numerator. In order to accumulate the
sum as far as possible in the R.R., it is necessary to move the carriage
as far to the right as possible. But
care must be taken to move the carriage only so far to the right that
space is left to accommodate the
most significant figures. Put the carriage in position 5.
Set decimal points between positions 2 and 3 in S.R.,
and positions 6 and 7 in R.R.
Step 1. Set the first term of the sum on the right hand side of
S.R. (00 . . . 9526.80).
One plus turn of the operating handle.
Step 2. Set 00 . . . 37.51 in S.R. One plus turn.
Step 3. Third term in S.R. One plus turn.
Sum in R.R. is now 10209.93. Clear only the C.R. and S.R.
Now follows the division by 3 by the breaking down method:
Carriage is in position 6. Set the divisor 3 in S.R. as far to
the left as possible, but not so far that a minus
turn would cause a negative number to be indicated in R.R.; i.e. set
3 in position 5. Place a decimal point
between positions 4 and 5 of S.R.
Place the reversing lever in its lower position.
With the operating handle pulled upwards we continue to subtract the
contents of S.R. from the contents
of R.R. until the latter indicates a negative number, i.e. until a
row of 9's appears (or possibly a row of 9's
and an 8); thus turn the handle in its minus position and observe
R.R. After 4 minus turns R.R. indicates
9 ... 8209930. Now make one plus turn; a row of 0's now
appears in R.R., and the number in R.R. is in
fact 0 ... 1209.930 ... 0. This number is the remainder after
dividing the original dividend by the number
now in C.R., i.e. 3, which is the most significant figure in the quotient.
Set the carriage in the next lower position, i.e. position 5.
Again turn the handle in its minus position until
a row of 9's appears in R.R., which occurs in this case after 5 turns.
Make one plus turn.
Carriage in position 4. Turn the handle in its minus position
until a row of 9's appears in R.R., as described
previously, and again one plus turn.
Carriage in position 3, 4 minus turns, one plus turn.
Carriage in position 2, 4 minus turns, one plus turn.
Carriage in position 1. Make one minus turn and zero appears in
R.R., which indicates that the division
is at an end. (In the case of a division where there is a remainder,
the remainder appears in R.R.) Check
that the number 3 (the divisor) is in R.R.
From the rule concerning decimal points in a division we have 6 (R.R.)
- 4 (S.R.) = 2 decimal places in
C.R. Thus we set a decimal point between positions 2 and 3 of
C.R. and read the result (i.e. the quotient)
as 3403.31. Return the reversing lever to its normal position.
By using a CURTA Model II (which has at
its disposal 8 places in C.R.) a quotient of 8 significant figures
may be obtained.
If, however, a large number of dividends are to be divided by
the same divisor, it is simplest to calculate
the reciprocal of the divisor once and for all, and place this quantity
as a constant multiplier in S.R. The
divisions are then transformed into multiplications, e.g.
1633 / 11.7
341.5 / 11.7
67.8 / 11.7
The division 1 / 11.7 to 6 or 7 figures gives us the reciprocal of the
divisor 11.7, namely 0.0854701. We
place this number in the right hand end of S.R., clear C.R. and R.R.,
and set a decimal point between 7 and
8 of S.R. The three divisions may now be carried out as three
normal multiplication, namely,
0.0854701 * 1633 = 139.572
0.0854701 * 341.5 = 29.1880
0.0854701 * 67.8 = 5.79487
An experienced computor will dispense with the intermediate clearing
of C.R. and R.R. after each
multiplication, and will build up the contents of C.R. to each successive
multiplier by appropriate plus and
minus turns of the handle.
First method (subtractive division)
Machine ready.
First we form the product 180 * 46 and then divide by 144. The
multiplication 180 * 46 is performed in
such a way that the product appears as far to the left as possible
in R.R.
Set the number 46 in S.R. by means of knobs 2 and 1. With the
carriage in position 6 make two plus turns
and in position 5 2 minus turns (short cut multiplication). The
product 8280.000 is now in R.R. (with three
decimal places in accordance with the decimal rule).
Now follows the division 8280 / 144 by the subtractive method (see the
previous example). Clear
only C.R. Set the number 144 in the right hand of S.R.
Place the reversing lever in the lower position.
The process of subtractive division now tales place with the carriage
starting in position 5. In this case
the division produces no remainder and the result (quotient)
in C.R. is 57.5.
Return the reversing lever to its normal position.
Second method
In numerous calculations involving the rule of three the calculation
of the intermediate quantity a / c is
also required; e.g.
If certain articles cost 180 francs/gross. how much does each article
cost, and how much do 46 articles
cost?
Machine ready.
First we must calculate the cost of one article (180 / 144) by additive
division, so the number 144 is set
in S.R. by means of knobs 3-1, and with the carriage in position 6,
the dividend 180 is built up figure by
figure in R.R. by positive turns of the operating handle. The
quotient appearing in C.R. is 1.25 = the cost
of one article.
Since we are about to multiply the cost of one article (1.25) by 46,
and the number 1.25 is already in
C.R., clear only R.R. Set the number 46 in the right hand
end of S.R. and place the reversing lever in
the lower position.
Starting with the carriage in position 4. reduce every figure in C.R.
to zero with plus turns of the handle.
This indicates a multiplication by 1.25, and the reduction of the contents
of C.R. to zero is a check. (See
the examples here , 34, 43.) The
result in R.R. is 57.50 francs, namely the price of 46 articles.
(Return the reversing lever to its normal position.)
The rule of three in a single calculation (only CURTA Model II)
In those cases in which the numbers involved are given only to a small
number of figures, the rule of
three may be affected at one blow by using a CURTA Model II, the quotient
being obtained with 4 or 5
figures.
![]()
Machine ready.
The division 1764 / 144 is carried out at the left hand end of R.R.
by the additive method. At the same
time the quotient of this division is multiplied by 375 in the right
hand end of R.R. S.R. 14400000375.
Place the carriage in position 5 and by turning the operating handle
in the appropriate manner build up
the number 1764 figure by figure in R.R. R.R. now reads 176400004593750
and C.R. 00012250. 1764
is the dividend 12.25 is the quotient 1764 / 144 and 4593.75 is
the final result (i.e. the product of
12.25 and 375).
![]()
Machine ready.
S.R. 34.40000087.2. Carriage in position 4. (Since the first
figure of the dividend is smaller than the first
figure of the divisor room for one more digit [i.e. position 15] in
R.R., must be left free.) Build up the
number 19.45 from the number 34.4.
R.R. 19.44976 0 49.30[288]. C.R. 000.5654.
Firstly, the division 325 / 12 is carried out by the additive method
to give 5 figures in the quotient; the
division is commenced with the carriage in position 5. The quotient
27.083 appears in the first 5
figures of C.R. Clear only R.R. Set 677 in the right
hand end of S.R. Place the reversing lever
to its lower position. Starting with the carriage in position
1 reduce the number in C.R. to zero by plus
tuns of the handle (see here ).
The product 18355.191 appears in R.R.
Carriage in position 6. Set the new divisor 119 at the right hand
end of S.R. Carry out the division by
means of the subtractive method as far as position 1 of the carriage.
R.R. now indicates a remainder of 0.028, C.R. indicates the quotient
154.077. (Replace the
reversing lever in its normal position.) By using this method
it is possible that a small rounding off
error can occur which, however, is insignificant in most practical
cases. If it is required to eliminate
this error completely, it is recommended that first the factors in
the denominator be multiplied
together and noted down, and secondly, the factors in the numerator
be multiplied together with the
product being accumulated as far to the left as is possible n R.R.
The divisor may then be set in S.R.
and the division carried out by the subtractive method.
In the method to be described it is supposed, that by means of a slide
rule or auxiliary tables or by
judicious guessing, an approximate square root has been found.
We wish to obtain a better
approximation.
Let N be the approximate value of R, the square root of
R**2, and denote the error in the approximation
by E, so that R = N + E. The method proceeds by
setting N in S.R., multiplying by N (which appears
in C.R.) to produce N**2 in R.R. The quantity 2N
is then set in S.R. (without clearing R.R. or C.R.), and
R**2 is built up from N**2 in R.R. Since
![]()
it follows that (if we neglect E**2) E
is added to C.R. Since C.R. already contained N, C.R. now
reads
N + E the new approximation.
The square root of 150 = ?
Initial approximation = 12.2.
Machine ready.
Carriage position 6. Set 12.2 in S.R. with knobs 3 to 1. Multiply by 12.2 starting from position 6.
Carriage position 6: 1 plus turn.
Carriage position 5: 2 plus turns.
Carriage position 4: 2 plus turns.
Set a decimal point between position 6 and 5 of R.R.: 148.84000.
S.R. Set twice the initial approximation (i.e. 24.4) in the same
positions as were used for the initial
approximation before. By turning the handle in the appropriate
manner in consecutive positions of the
carriage, increase the number in R.R. to 150, thus
Carriage position 4: 1 plus turn.
Carriage position 3: 5 minus turns.
Carriage position 2: 3 minus turns.
Carriage position 1: 5 plus turns.
R.R. now reads 149.999.
C.R. now gives to 6 correct figures the root 12.2475.
This method determines as many additional correct figures as there were
correct figures in the
approximation. In this case the initial approximation is correct
to three figures, and the desired
approximation to 6 figures. From this rule it is unnecessary
to proceed further; furthermore we have
in this particular case come very near to the required number (150)
with 149.999.
If one requires 8 correct figures in the root and a CURTA Model II is
available, one can repeat the
previous example using the initial approximation 12.25 (i.e. with 4
correct figures). One then obtains
the root 12.247449 in C.R.
Remark: The rule that one gains as many correct figures in the root
as one has to start with is capable
of a limited number of exceptions. (See page 49 same method by
subtraction.)
Cube roots
CURTA users who have at their disposal our CURTA Tables may, by use
of these tables, obtain a
cube root correct to 5 figures by means of an addition and one subsequent
multiplication. These
tables will be forwarded free of charge on application to our headquarters.
Use of tables can be avoided by using an extension of the method for
obtaining square roots as
described in the last section.
Let N be the approximate value of R, the cube root of ![]() ,
and denote the error in the approximation
,
and denote the error in the approximation
by E, so that ![]()
The computation proceeds by arriving at a situation in which we have ![]() in R.R.,
in R.R., ![]() in S.R.,
in S.R.,
and N in C.R. We then build up the contents
of R.R. to ![]() ,
i.e. from the above equation, adding
,
i.e. from the above equation, adding
approximately E to the contents of C.R. C.R.
thus contains a quantity which approximates to N + E.
It will be appreciated that (and this remark applies equally well to
the method for deriving square
roots) if the derived approximation is insufficiently accurate, it
may be improved by repeating the
process.
The cube root of 132.651 = ?
Machine ready.
Initial approximation = 5.0.
Carriage in position 6: Set 5 in S.R. with knob 1.
Multiply by 5 in position 6.
R.R.: 25. Set a decimal point in C.R. between positions
5 and 6.
Clear C.R. and R.R. Set 25 in S.R. with knobs 2 and 1.
Multiply by 5 in position 6. Replace 25 in S.R. by 75 (= 3 *
25).
Increase the contents of R.R. to 132.651, thus
Carriage in position 5: 1 plus turn.
Carriage in position 3: 2 plus turns.
Carriage in position 1: 1 plus turn.
R.R. now contains 132.65075. C.R. contains 5.10201.
The cube root of 132.651 is 5.1. If the
process is repeated with the first approximation 5.10201, C.R.
finally contains 5.1.
Further roots may sometimes be computed by application of the preceding methods, e.g.
The sixth root of 14 = ?
Firstly, we compute the square root 3.74166 and then the cube root of
this number, namely
the sixth root of 14 = cube root of 1.5524.
Continued multiplication
a * b * c * d * . . . etc.
Introductory remark: The limit of a computation of this type
is reached when the number of figures
in the product is equal to the number of figures in the Result
Register, i.e. 11 figures for the CURTA
Model I and 15 figures for the CURTA Model II. Before the
computation is begun it is possible to
estimate the number of figures in the different factors. One
can, if the need arises, omit the last figures
of the partial products in order to avoid an excessively long end product.
Obviously, one can compute a function of the form a * b * c *
d * . . . etc. by multiplying the first two
factors together, setting the product in S.R., multiplying by the third
factor, and so on. Use of this
method, however, means that each partial product must be set at each
stage into S.R. We now
describe two methods which may readily be applied in many cases.
First Method
38 * 24 * 57 * 63.44 = ?
Machine ready.
I. S.R.: Set the number
38 with knobs 2 and 1.
C.R.: Develop
24 (normal multiplication).
R.R.: Result
912 = partial product I.
II. S.R.: Set the next factor diminished by a tenth, i.e. 56.9 = (57 - 1/10th) with knobs 3 to 1.
Carriage: Place the last figure on the right of S.R. immediately
under the first figure on the left of the
partial product in R.R., thus move the carriage to position 3.
Handle: Continue to turn the operating handle in its plus position
until the number immediately above
the 9 in S.R. goes to 0. One thus observes this number in R.R.
and continues to turn the handle until it
reads 0 (optical control). 513 012 now appears in R.R.
Carriage: Position 2. One observes the second place in R.R.;
after one plus turn this indicates a 0.
R.R. now reads 518 702.
Carriage: Position 1. One observes the first figure of R.R.;
this indicates 0 after 2 plus turns. R.R.
then reads 519 840. The partial product II is 51
984.0 (because 56.9 was set instead of 57 which gives
one decimal place in R.R.). The partial product II was derive
as follows:
(56.9 * partial product I) + 1/10th
partial product I = 57 * partial product I
III. S.R.: Set the number 63.439 = (63.44 - 1/10th) with knobs 5 to 1. (minus 1/10th in last digit)
Carriage: Position 6. Turn the handle in its plus position
and at the same time observe the 6th position
of R.R. When this reaches 0 R.R. reads 31 720
019 840.
Carriage: Position 5. When the 5th number in R.R. has ben
reduced to 0, R.R. reads 32 354 409 840.
Proceed in this manner from position to position up to and including
position 1 of the carriage. Finally,
R.R. indicates 32 978 649 600. The final product, after
bearing in mind the three decimal places of the
number, is thus 3 297 864.96.
Remark: It can occur that the number of figures in the partial
product is greater than the number of
positions through which the carriage may be moved. The next example
shows nevertheless, that the
same method can still be used. It is, however, advisable to arrange
the computation in such a manner,
where possible, that the factor with the largest number of figures
is set last in S.R. (see the first
example).
63.44 * 38 * 24 * 57 = ? (the result is already known).
The multiplication 63.44 * 38 = 2410.72
is
normal. Next set 23.9 in S.R., with knobs 3 to 1.
Carriage: Position 6. By turning the handle in its plus
position in positions 6, 5, 4, 3, 2 and 1 of the
carriage, reduce every digit in R.R. to 0. R.R. now reads
57 857 280. The partial product is 57 857.280.
Continuation of the calculation with a CURTA Model I.
Carriage: Position 6.
S.R.: Set 56.9 with knobs 5 to 3 (knobs 1 and 2 to
0). By turning the handle in its plus position in
positions 6 to 1 of the carriage reduce each digit in turn to
0 (first the 8th digit, then the 7th digit, and
so on). The second and first digits of R.R. are not reduced to
0. R.R. now reads 3 297 860.4080. We
can identify this result with that produced in the previous example.
If complete accuracy is required
for the last two figures the computation may be conducted as follows:
S.R.: Set 56.9 with knobs 3 to 1 (knobs 4 and 5 to 0).
Carriage: Position 2. By turning the handle in its plus
position reduce the digits in positions 8 to 2 to 0.
Carriage: Position 1. This digit is already 0, the
calculation is finished. R.R. reads 3 297 864.9600.
Continuation of the calculation with a CURTA Model II.
The carriage of the CURTA Model II may be moved through 8 positions,
and in this instance the
calculation in hand may be completed in the normal manner as described
in I.
However, as an exercise for the case in which the number of figures
in the partial product exceeds the
number of positions through which the carriage may be moved, and in
order to fully appreciate the
principle described, it is advisable to carry out the exercise given
for the CURTA Model I. We
therefore request you to perform the previous method on your CURTA
Model II. The end result in
R.R. is the same as before.
Second Method
38 * 24 * 57 * 63.44 = ?
Machine ready.
Proceed as for section I of the previous example. This method
differs from the previous one in that
the next factor is reduced by a unit in the last figure instead of
by a tenth. Thus set 57 - 1 = 56 in
S.R. with knobs 2 and 1.
Clear only C.R.
Carriage: Position 3.
Handle: The arrow points to 9 in R.R. Memorize this number
and carry out 9
plus turns of the handle. Naturally, a 9 appears in C.R.
Carriage: Position 2. The arrow now points to a 1 in R.R., thus one plus turn of the handle.
Carriage: Position 1. The arrow points to a 2 in R.R., thus
two turns of the handle. R.R. shows partial
product II, namely 51 984, and C.R. indicates partial product
I, namely 912. Set in R.R. the third factor
minus a unit, namely 56. Partial product II was arrived
at as follows:
(56 * Partial product I) + (1 * Partial product
I), (which was already in R.R.) = 57 * Partial product
I.
Clear only C.R., and set in the right hand end of S.R. the factor 63.44
with the last figure diminished by
a unit, i.e. 63.43. Beginning with the carriage in position
5 turn the handle in its plus position so as to
build up in C.R. the number now in R.R. The final result
indicated in R.R. is 3 297 864.96.
The advantage of this second method is that no zeros appear at the right
hand end of R.R., and thus
the full capacity of the machine can be utilized. It is, however,
necessary to check the calculations by
noting that the partial products appear in C.R., whereas in the first
method this was automatically
assured by the appearance of a 0 in the successive positions
of R.R.
We first obtain 327**2, i.e. 327 * 327 by normal multiplication.
The square 106 929 is built up in R.R.
S.R. indicating 327 and C.R. also indicating 327 are not cleared.
C.R. will now be built up to 106 929 starting with the carriage
in position 6 in order that the least
significant figures in R.R. will not be modified in the ensuing multiplications.
Carriage: Position 6. The arrow points to a 1
in R.R. In the corresponding position of C.R. there is a 0;
thus one plus turn.
Carriage: Position 5. The arrow points to a 0.
In position 5 of C.R. there is similarly a 0. Thus this
position can be skipped over.
Carriage: Position 4. The arrow points to a 6
in R.R., thus turn the handle in its plus position until C.R.
also indicates a 6 in this position.
Carriage: Position 3. The arrow points to a 9
in R.R. Thus turn the handle in its plus position until the
3rd position in C.R. also indicates 9.
Carriage: Position 2. In this position both R.R. and C.R.
indicate a 2. Thus this position can be skipped
over.
Carriage: Position 1. In this position R.R. indicates a 9, and C.R. a 7; thus two plus turns.
Now the basic number 327 is in S.R., in C.R. the square
106 929, and in R.R. the 3rd power
34 965 783.
Higher Powers
Clearly the capacity of the machine used limits the order of the power
to be computed. In the previous
case for example the fourth power may be computed with a Model I by
setting the cube and multiplying
by 327. With the result 11433811041 the limit of
the capacity or R.R. is reached. Higher powers may
be computed only by discarding the last 3 or 4 figures in S.R.
Using the Model II the fourth power also may be computed without clearing
S.R. and C.R. by
developing the approximate number in C.R. in a manner similar to that
which has been described in the
third power, the cube being fully contained in C.R. For higher
powers it is suggested that some
convenient number (square, 3rd power, etc.) be set in S.R., in which
case, when larger numbers are
being dealt with, the necessity for curtailing the number is indicated
in advance.
![]()
+ 6925
6925**2
+ 3289
3289**2
- 1721
1721**2
+ 2987
2987**2
s = ?
S = ?
Machine ready.
Move the clearing lever to the left hand end of R.R. Set
decimal point between positions 11 and 10
of R.R. Set a 1 with knob 11 and the
number 6925 with knobs 4 to 1 in S.R. Develop
6925 with the
handle.
In C.R. there now appears the number 6925, on the right of
R.R. the square 47 955 625 and
on the left of R.R. as a check the multiplier 6925.
Clear only the left hand end of R.R.; i.e.
move the clearing lever only over the number 6925 as far
as the 0 and return it to its original
position.
Set the next number, i.e. 3289, at the right hand end of S.R.
(retaining the 1 in position 11). Develop
3289 with the handle so that the digit in S.R. generates the
multiplier at the left of R.R. and acts as a
check.
We have now accumulated the sum of the first two numbers in C.R., and
the sum of the first two squares
at the right hand end of R.R. As a check the multiplier
3289 is at the left hand end of R.R. Again we
clear only multiplier 3289 at the left hand end
of R.R.
Set the next number in the right hand end of R.R. Since the sum
is being accumulated in C.R. we move the
reversing lever to its lower position. Develop the number
1721 normally with the handle. Again
clear only the left hand end of R.R., (i.e. the multiplier 1721).
Move the reversing lever to its normal
position. Set the next number at the right of S.R. and
multiply it by itself.
The final result at the right hand end of R.R. is 70 657 156 = S, and in C.R. we have 11 480 = s.
At the left of R.R. the last number 2987 stands as a check.
You may again partially clear so that the sum
S remains by itself for further calculations.
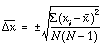
In order to facilitate the calculation we reduce each observation by
a known constant x0 and in this
manner reduce the number of figures in the numbers used in the calculation.
We have
![]() and
and ![]()
The calculation can be carried out by the CURTA in the following manner,
where the capacity of the
Model II is always sufficient. If the number of figures in, and
the dispersion of, the observations are not
too large, the CURTA Model I may also be used, as the following example
indicates:
Machine ready.
S.R.: 005.30001; Carriage in position 3.
Multiply by 5.3 and clear only C.R.
To mark the decimal points always use the white movable markers.
S.R.: 006.40001; Carriage in position 3. Multiply
by 6.4. Clear only C.R. After these two steps we
have in R.R.:
069 , 05 / 0 / 11 , 700
i.e.
![]()
Proceed in this manner, and after 7 such steps we have in
R.R.: 252 , 84 / 0 / 41 , 200
or ![]()
Clear only C.R.
Set in S.R. ![]() and N, thus: 041.20007.
and N, thus: 041.20007.
Carry out the division 41.2 / 7 in the right hand part
of R.R. by the subtractive method. Thus move the
reversing lever to its lower position and commence the division with
the carriage in position 4. When the
division is finished C.R. indicates 005.885, that is: ![]()
The mean value of the observations is thus ![]()
R.R. contains 0.1037800005. Up to the last 5
(which is the remainder of the division) that is:
![]()
Clear only C.R. Carriage in position 6.
S.R.: Set N(N-1), i.e. 0.42.00000, in
S.R. Carry out the division ![]() by the subtractive method.
by the subtractive method.
Result in C.R.: 0.247.
By means of a slide rule or a CURTA the square root of this number is
found to be 0.497. The observation
measurement reads finally: ![]()
(Return the reversing lever to its normal position.)
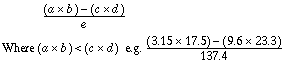
![]()
Machine ready.
S.R.: Set 3.15 at the extreme right. Set a
decimal point in front of knob 2 of S.R.
Carriage in position 4: Normal multiplication by
17.5 in positions 4, 5 and 6 of the
carriage.
R.R.: . . . 55.125 . . . Set decimal points in front of
position 4 in C.R. and position 6 of R.R.
Clear only C.R.
S.R.: Set 9.6 with knobs 3 and 2. Set knob 1 to zero. Place the reversing lever in its lower position.
Develop 23.3 in C.R. by turning the handle in its minus
position in positions 4, 5 and 6 of the carriage
(negative multiplication).
R.R.: . . . 99831.445 . . . = Complement of the dividend.
Do not clear R.R.
Division by e
This division is carried out by building up the dividend to zero by
means of the divisor. Return the
reversing lever to its normal position. Clear only C.R.
Carriage in position 6.
Set 137.4 in S.R. with knobs 4 to 1.
Set decimal points in front of knob 1 in S.R. and in front
of position
5 of C.R. By turning the handle force the contents of R.R.
as near zero as possible, i.e. to 9999 etc.
Thus observe R.R. and in:
Carriage
position 6: 1 plus turn
Carriage position 5: 2 plus turns
Carriage position 4: 2 plus turns
Carriage position 3: 7 plus turns
Carriage position 2: 3 minus turns
Carriage position 1: 5 plus turns
There is now in R.R. the nearest possible approximation to zero
(0.000450).
The answer -1.22675 stands in C.R.
To find:![]()
![]()
![]()
We first compute the divisor and note it down. The dividend is
then formed as far to the left as possible in
R.R. and finally, by setting the divisor in S.R., subtractively divided.
Machine ready.
Set the quantity 2 * 16.78, i.e. 33.56, in
S.R. and multiply by 13.63. The result 457.4228 is
noted down.
Machine ready.
Set the number 16.78 in S.R. by means of knobs 8
to 5: 00016780000. Develop 16.78 in C.R.
as
follows:
Carriage in position 5: 2 minus turns
Carriage in position 6: 2 minus turns
Carriage in position 7: 2 minus turns
Carriage in position 8: 2 plus turns
Clear C.R. only. Set a decimal point between positions
12 and 13 of R.R. Set the number 13.63
in
S.R. with knobs 8 to 5: 00013630000, and develop
the number 13.63 in C.R. in positions 5 to
6.
R.R. now contains the sum of the first two squares: 467.3543.
Clear C.R. only. Set the number 20.33 in S.R.
with knobs 8 to 5: 0020330000. Place the
reversing
lever in its lower position. Develop 20.33
in C.R. by turning the handle in its minus position in positions
5 to 8 of the carriage (negative multiplication).
In R.R. the third square has been subtracted from the sum
of the first two and the result is the dividend 54.0364.
Clear C.R. only. Place the carriage in position 8. Set the
divisor 457.4228 (previously noted down) in S.R.
with knobs 7 to 1: 00004574228, and set a decimal
point between knobs 5 and 4. Now follows the
division by the subtractive method (see
here).
The final result in C.R. after applying the decimal point rule
is ![]()
(Return the reversing lever to its normal position.)
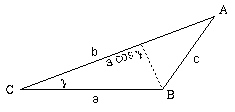
Given: find c = ?
find c = ?
Direct use of the classical formula ![]() is computationally inconvenient, due to
is computationally inconvenient, due to
the large size of the numbers involved. The best method of procedure
is as follows:
1. Obtain the values ![]() .
.
2. Compute ![]()
3. Then by Pythagoras' theorem ![]()
Machine ready.
To mark the decimal points always use the white movable markers.
S.R.: 21.47. Develop 0.532712 in C.R. with the handle.
R.R.: ![]() .
Note this number down and do not clear.
.
Note this number down and do not clear.
C.R.: By turning the handle change the contents to 0.846296.
R.R.: ![]() . . ., not cleared.
. . ., not cleared.
Carriage position 6.
S.R.: Set b = . . . 32.14 to correspond with the number
in R.R.
Handle: 1 minus turn. If ![]() a complement appears in R.R., which is the case with the present example.
a complement appears in R.R., which is the case with the present example.
S.R.: Set the modulus of the number in R.R. (If ![]() ,
then set the number in R.R.) In the present
,
then set the number in R.R.) In the present
example the number (rounded off) is . . . 13.970. As a check
carry out one plus turn when R.R. reads
(1)0000 . . . or 9999 . . . Clear R.R. and C.R.
Finally, multiply the number in S.R. by itself, thus
13.970 * 13.970.
R.R.: ![]()
Clear C.R. only.
S.R.: ![]() .
Multiply by 11.437.
.
Multiply by 11.437.
R.R.: ![]()
Now compute the square root by Hermann's method (see here) or any other appropriate method.
The result is 18.054 in. = c.
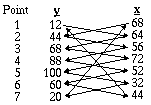
The area to be computed is defined by the following co-ordinates, which
are juxtaposed for the purpose
of calculation.
The calculation follows from the general formulae ![]()
First we develop![]() in C.R. by means of the handle. Now set
in C.R. by means of the handle. Now set![]() in S.R.,
in S.R., ![]() must
be multiplied by
must
be multiplied by
![]() , thus
, thus
C.R.: Develop 12.
S.R.: Set 64 at the extreme right.
C.R.: By means of the handle change to 68 (difference between![]() and
and ![]() ).
).
The arrows in the following scheme indicate the further course of the
calculation.
S.R.: 72;
C.R. by means of the handle change to 100.
S.R.: 32;
C.R. by means of the handle change to 20.
S.R.: 68;
C.R. by means of the handle change to 44.
S.R.: 56;
C.R. by means of the handle change to 88.
S.R.: 56;
C.R. by means of the handle change to 60.
S.R.: 44;
C.R. by means of the handle change to 12.
R.R. contains 3856 = 2F. F = 1928.
If the number of points given is even, then in practice we enter the
last point twice. The area contributed
by the existence of the added point is zero, and the validity of the
scheme adopted is unaffected.
Depending on the order chosen in which to traverse the points, it may
occur that the final result in R.R.
is negative. The correct result in this case is the complement
of this number. The given example is
sufficient to establish the principle employed in calculating areas
with the machine. The same principle
also applies when the points lie in differing quadrants, but the sign
convention must very strictly be
obeyed.

The co-ordinates of the points A and B are known.
We wish to find the distance ![]() .
.
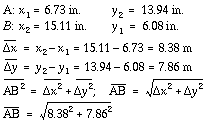
Machine ready.
Set a decimal point between knobs 3 and 2 of
S.R. Set 8.38 at the right of S.R. With the carriage
in
positions 4 to 6 develop the number 8.38
in C.R. by means of the handle. Set a decimal point between
positions 8 and 7 of R.R. The product
in R.R., 70.2244. will be accumulated with the next product
(7.86 * 7.86), and is therefore not cleared.
Clear C.R. only.
Set 7.86 at the right of S.R. With the carriage in
positions 4 to 6 develop the number 7.86
in C.R. by
means of the handle. R.R. now contains the sum of the two squares:
132.004. This number is not
cleared.
Clear C.R. and S.R. only.
The square root may now directly be computed by Hermann's method (see
here). The calculation here,
however, involves a subtraction. Thus move the reversing lever
to its lower position. First
approximation 11.5.
Carriage in position 6. Set the first approximation
11.5 in S.R. with knobs 5 to 5. Develop the
number
11.5 in C.R. by turning the handle in its minus position with
the carriage in positions 6, 5, and 4.
S.R.: Change knobs 5 to 3 to 230
and in positions 3, 2, and 1 of the carriage
use the handle to bring
the number in R.R. as close to zero as possible. C.R. then indicates
the square root 11.4893 (R.R.
contains 0.0001). The length ![]() =
11.49 in.
=
11.49 in.
(Return the reversing lever to its normal position).
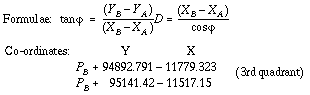
![]()
Machine ready.
(To mark the decimal points always use the white movable markers.)
Carriage: Position 7.
S.R.: 00094892.791 1 plus turn
S.R.: 00095141.420 1 minus turn
R.R.: 999751.371 . . . =
complement of ![]()
Do not clear R.R.
![]()
Carriage: Position 1.
S.R.: 00011779.323 1 minus turn
S.R.: 00011517.150 1 plus turn
R.R.: 999751.371 (see NOTE) / 737827
/
NOTE: Use two contiguous markers here.
737827 = complement of ![]() .
.
S.R. . . . 262.173 = absolute value of ![]() .
1 plus turn.
.
1 plus turn.
R.R.: 999751.371 . . . = complement of ![]() .
.
Clear C.R. Note down the absolute value of 248.629.
![]()
(Division by using the divisor to bring the contents of R.R. up to
zero (see here)).
Reversing lever in its
normal position.
Carriage in position 7: 1 plus
turn
Carriage in position 6: 1 minus
turn
Carriage in position 5: 5 plus
turns
Carriage in position 4: 2 minus
turns
Carriage in position 3: 4 plus
turns
Carriage in position 2: 7 minus turns
Carriage in position 1: 9 plus
turns
![]()
Do not clear S.R.
![]()
Clear C.R. and R.R. only.
Carriage in position 7. 1 plus turn.
R.R.: 000262.173 . . . = Dividend .
S.R.: . . . 0.725601. Carriage in position 6.
Clear C.R.
Move the reversing lever to its lower position.
Carry out subtractive division.
C.R.: 000361.318 = D.
![]()
Machine ready. ![]()
Carry out the division 248.629 / 0.688116.
C.R.: 361.31844. D = 361.318.
Example: to find ![]()
From tables: ![]() Since the argument is in steps of
Since the argument is in steps of ![]() ,
we must
,
we must
interpolate using as argument 14/60 = 0.233. (An
experienced computer will carry out the division by 60
in his head).
Set ![]() at
the right hand end of S.R., and in C.R. a decimal point between positions
3
at
the right hand end of S.R., and in C.R. a decimal point between positions
3
and 4. Develop 0.233 in C.R. with the handle.
Clear neither R.R. nor C.R.
Set ![]() in
S.R., and complete the number in C.C. to 1.000 (multiplication by
1-0.233).
in
S.R., and complete the number in C.C. to 1.000 (multiplication by
1-0.233).
We find the required value in R.R.: 0.29624(945). Thus,
rounding to 5 figures, we have:
![]()