Latest News
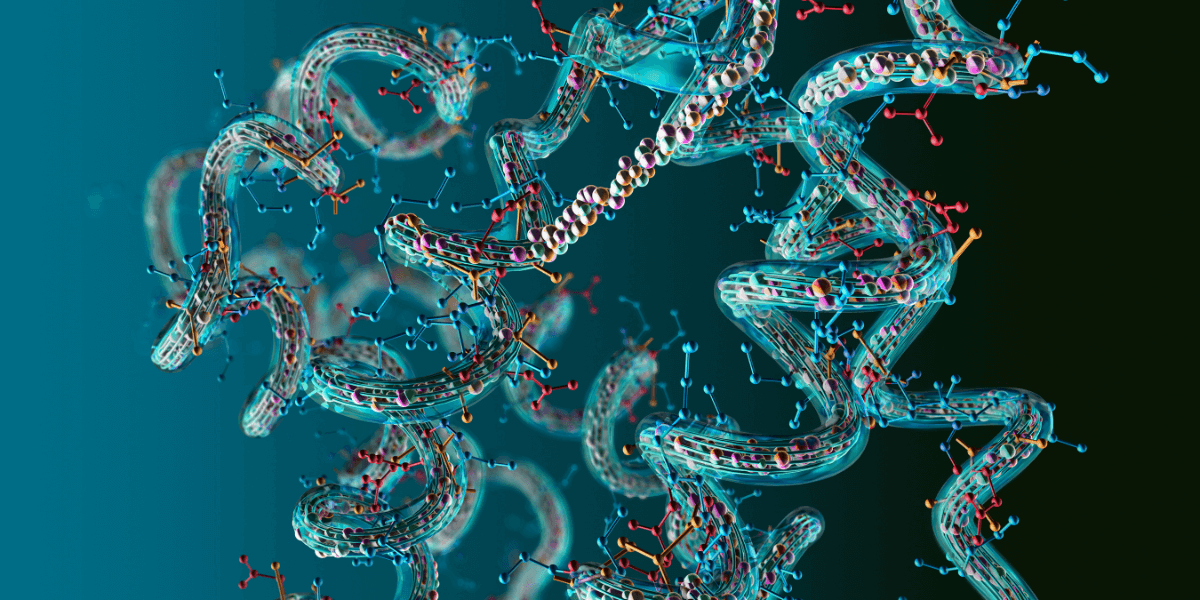
ISI Researchers Pioneer Developments In Protein Data Bank
ISI researchers are part of a core team developing the PDB-Dev repository, initiated by the Protein Data Bank, a foundational repository for macromolecular structures

Inside ISI’s Ph.D. Visit Day 2024
Prospective graduate students traveled to ISI’s Marina Del Rey headquarters to experience the institute’s academic environment.

To “Howdy,” or Not to “Howdy,” That Is the Question
USC researchers explore the impact of prompt design on large language model performance.
UPCOMING EVENTS
Apr
18
NL Seminar-DeLLMa: A Framework for Decision Making Under Uncertainty with Large Language Models
Ollie Liu, USC
-
Apr
19
AI in Structural Biology: Roots of Success
Dr. Helen Berman, USC
-
Apr
25
NL Seminar- How to Steal ChatGPT’s Embedding Size, and Other Low-rank Logit Tricks
Matthew Finlayson, USC
-
